入試問題・模試問題 解説等
来年以降、化学受験を考えている人たちへ
今回の共通テストの解答と解説を載せましたが、どうしてこう考えるのか? といった解説があった方がいいですね。
このように出来たら、またここにアップしたいと思います。
さて、共通テストも2回目が終わりました。(第2日程の分もありましたね)
今までのセンター試験と問題がどう変わってきたのか、
これからの勉強方法はどうすればいいのか、について書いてみたいと思います。

化学、化学基礎についてですが、
これまでのセンター試験では、たくさんの過去問やそれに類する問題を出来るだけ多く解く。
素早く正確に解けるようにする。
この勉強法で高得点、満点を狙えました。
共通テストでもこの勉強方法で間違ってはいないと思います。
でも、共通テストが始まる前に公開された「試行問題」の中にあったような「思考させる問題」が本番でもやはり多めに出題されています。
この「思考させる問題」は、予想していたよりそれほど難しい内容ではないものの、こういう問題には試験本番の時初めて出会うということになるでしょう。
見たこともない問題に出会うだけで焦りますし、その分時間のロスになったりします。
この手の新しい問題に対して、どう勉強していけばいいのでしょうか?
まずは、今までの勉強法を見直しましょう!
今までは、「問題を沢山解いて慣れればいい。沢山解くほど慣れていく」
というスタンスで勉強してきませんでしたか?
確かに、同様の問題を沢山解くことによって、素早く正解が出せるようになってきたでしょう?
しかし、冷静に考えてみると・・・
慣れてきたということは、「今までのやり方を間違えずに早く出来るようになった」ということなんですね・・・!
「深く考えるようになった」というのではちょっとないのです。
もちろん、慣れて余裕が出来る分、他のことを考えられるようになるとかはありますが。
さあ、どうすればいいのでしょうか?
いつも、
「常に原理等を考えながら解く! そして、考えることに慣れよう!」
というのが自分からの提案です。
中和滴定の公式の意味も考えておく、とか、酸化数の原理は何だろうとか。
もう一つ、感じたことを書いておきます。
現行の共通テスト向けの問題集、そして模擬試験、予想問題集についてです。
「思考させる問題」について対策がされていて色んな問題が出題されていますが、
各社とも気張ってしまっていて、凝った問題になり過ぎているのではないかと強く感じています!
もっと基本的な思考問題を沢山解いていった方がいいのではないでしょうか?
「思考問題」対策に気を配りすぎずに、常に考えながら問題を読み解くクセをつけた方がいいと感じています。
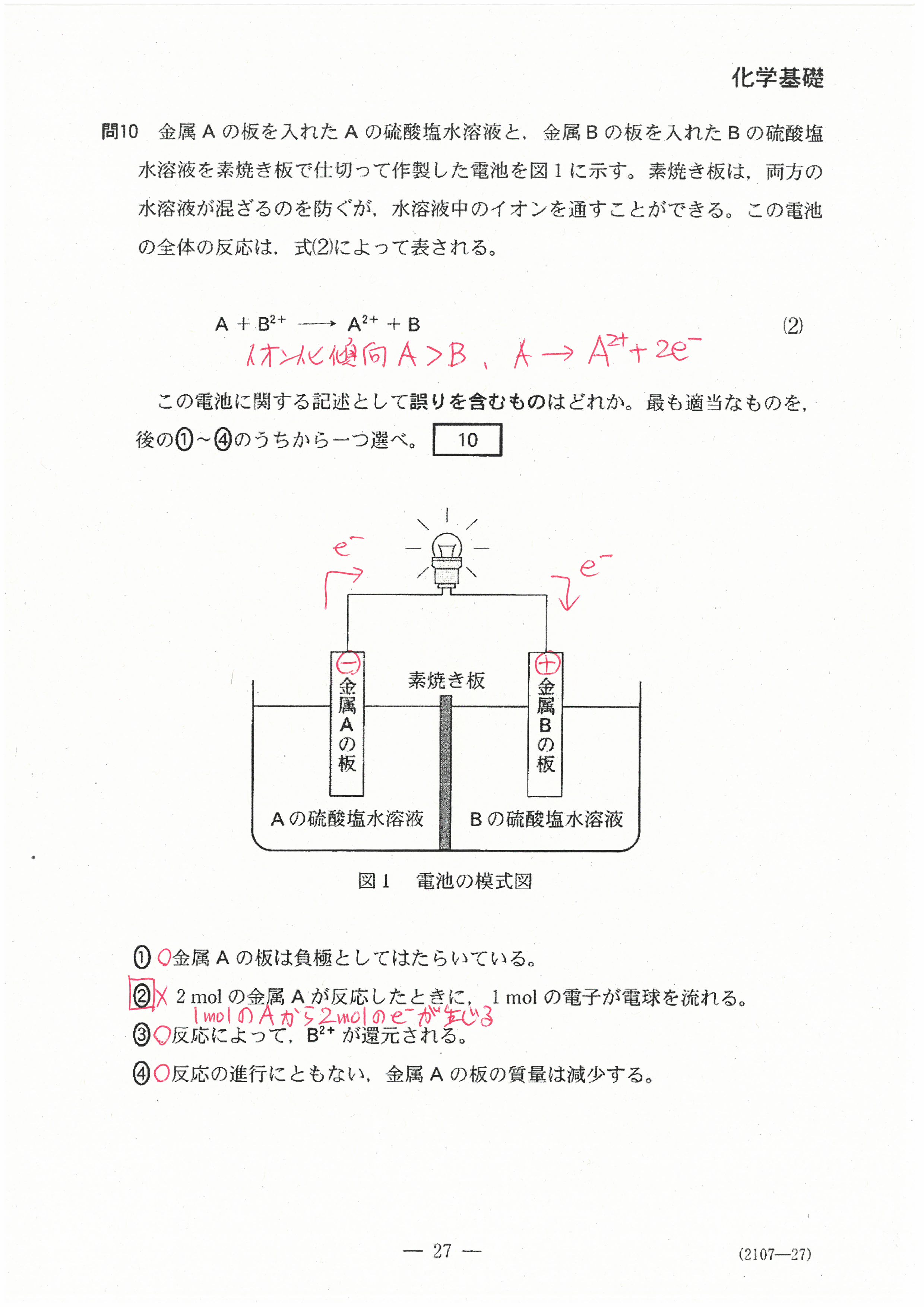
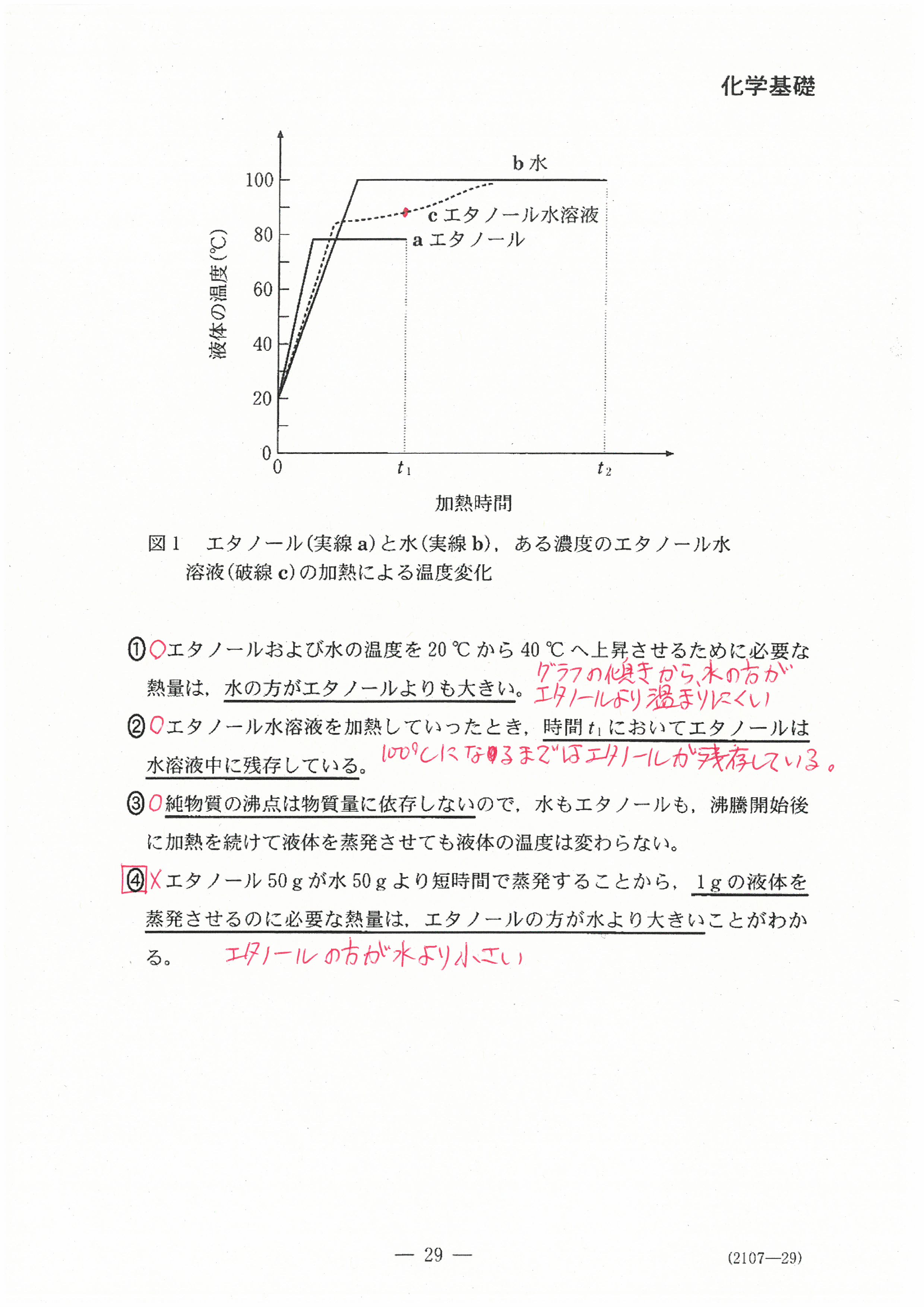
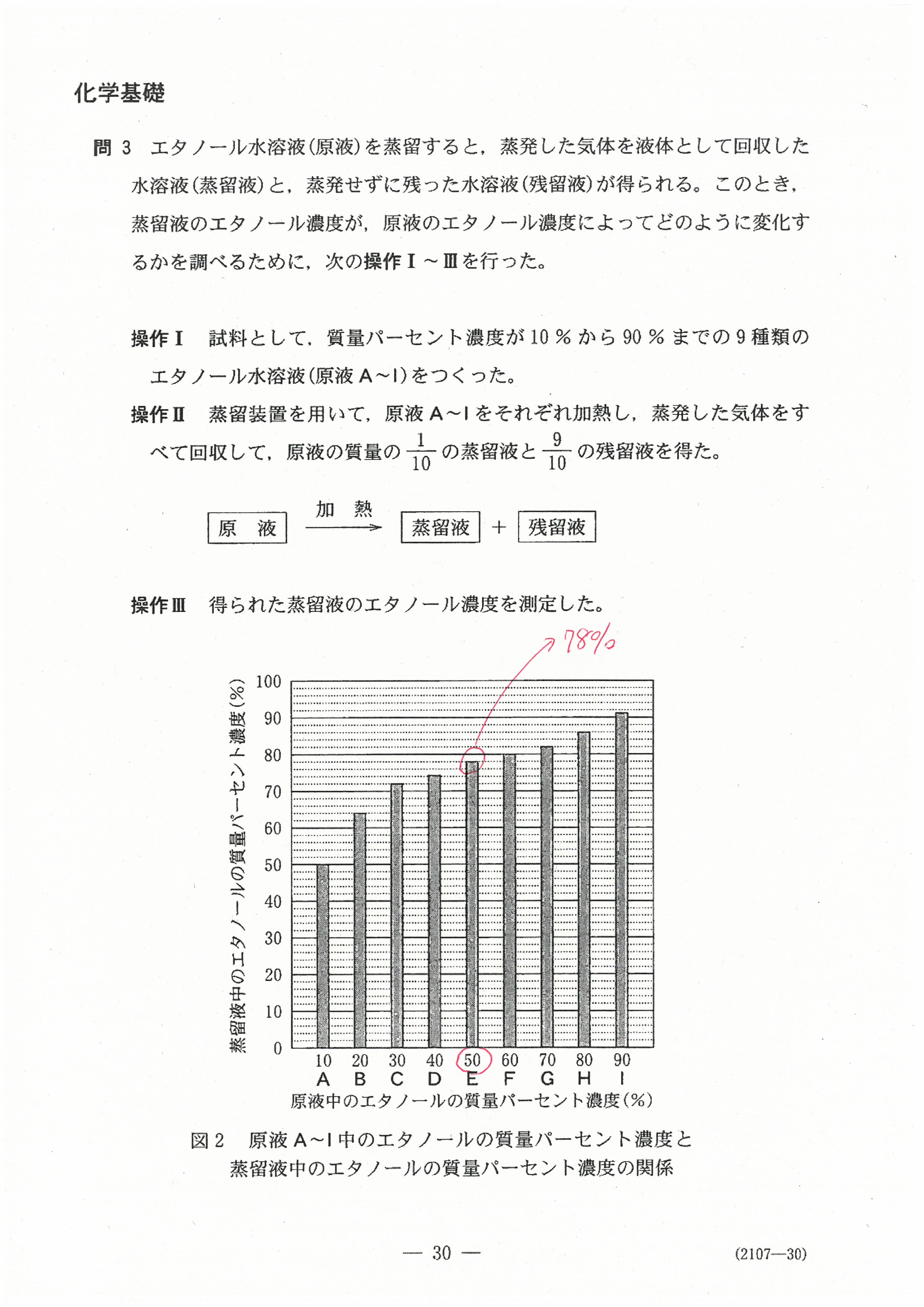
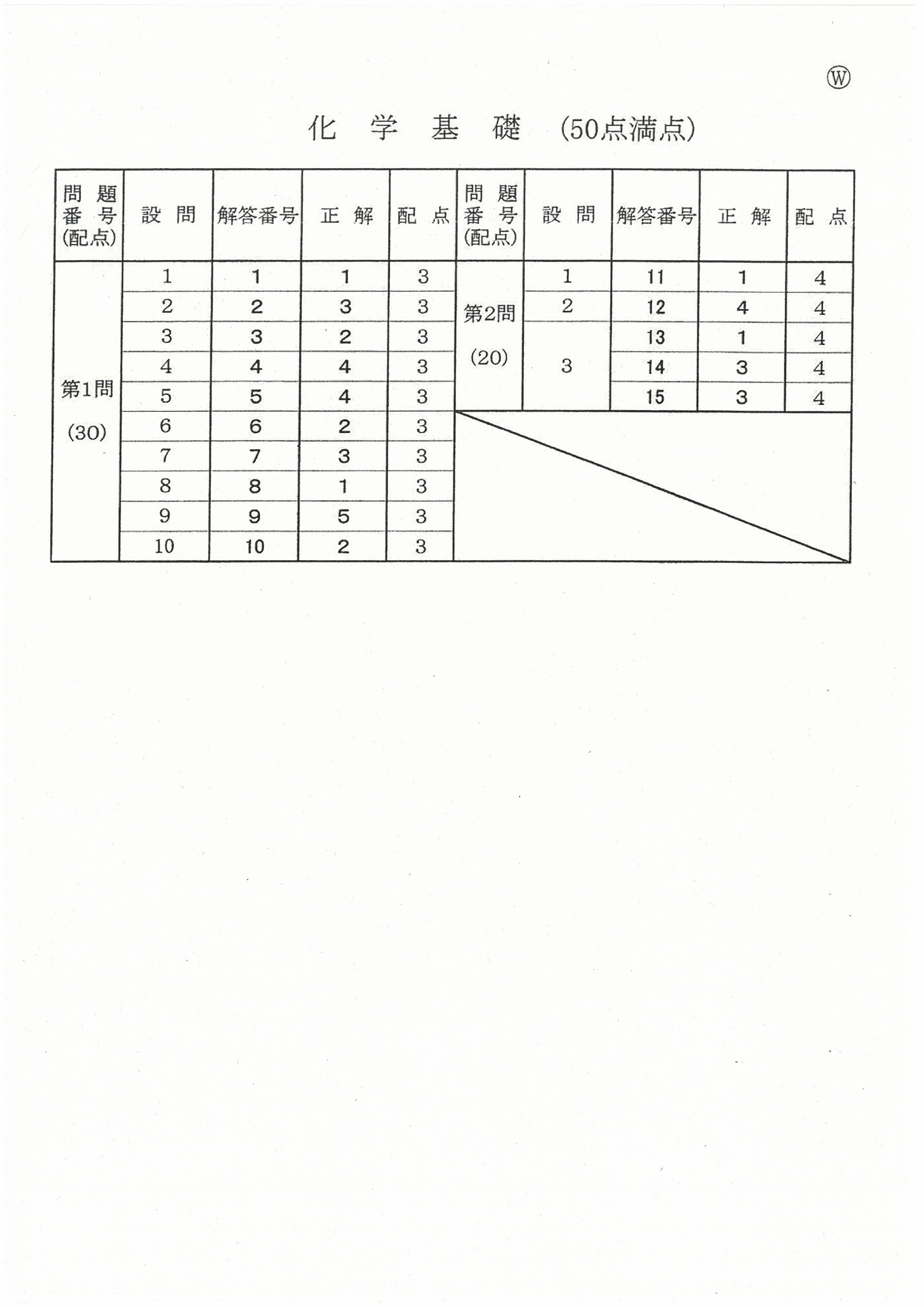
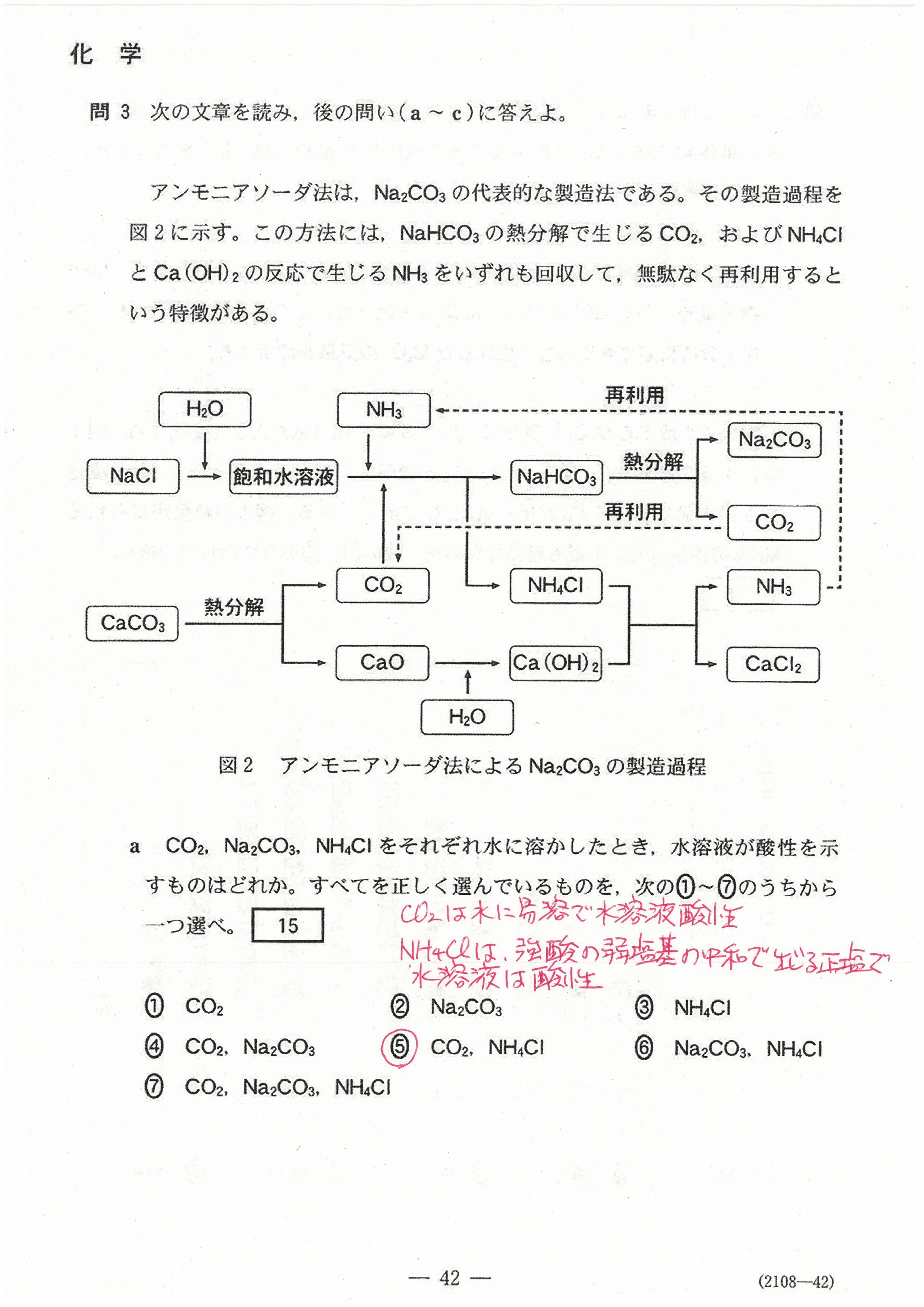
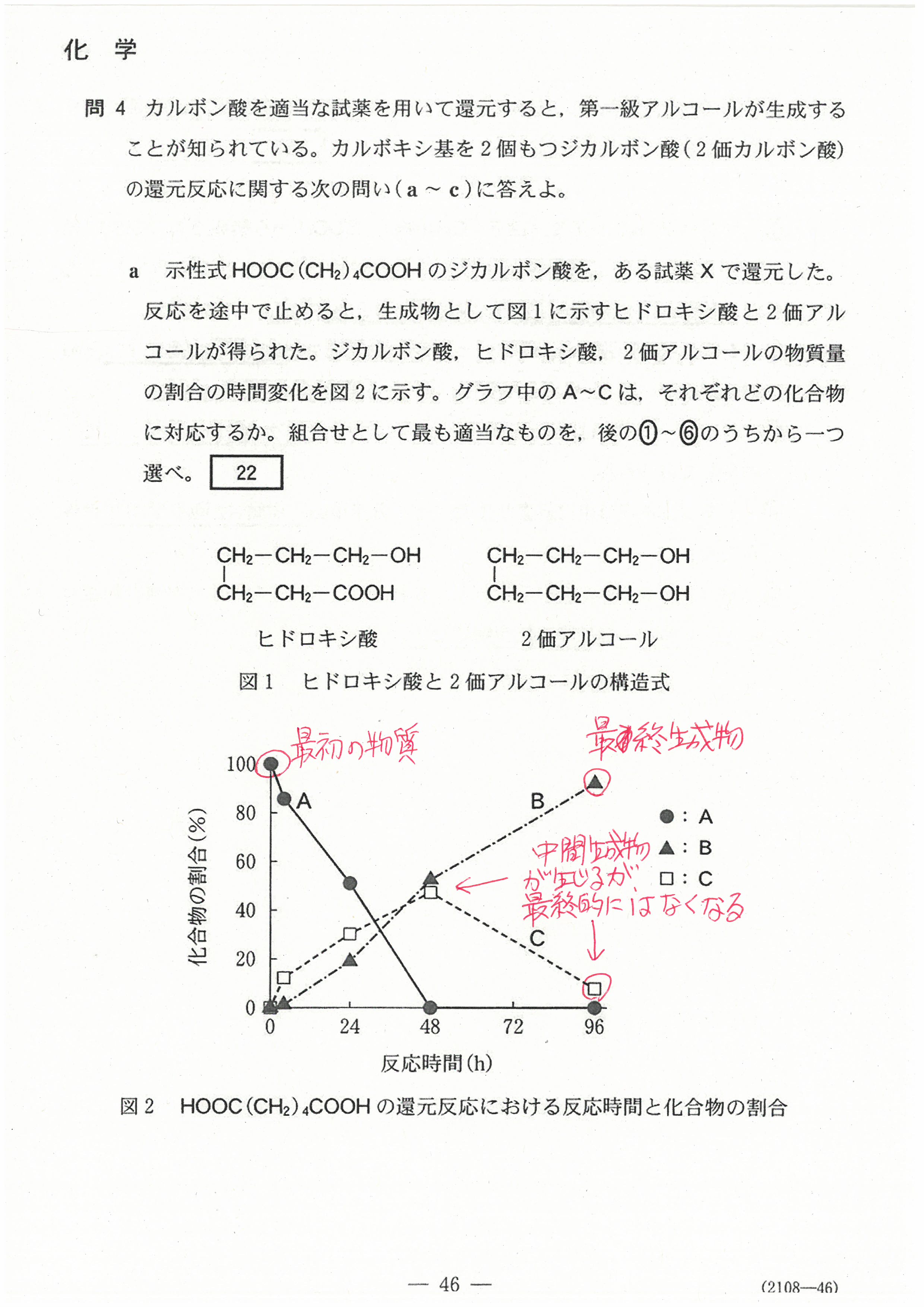
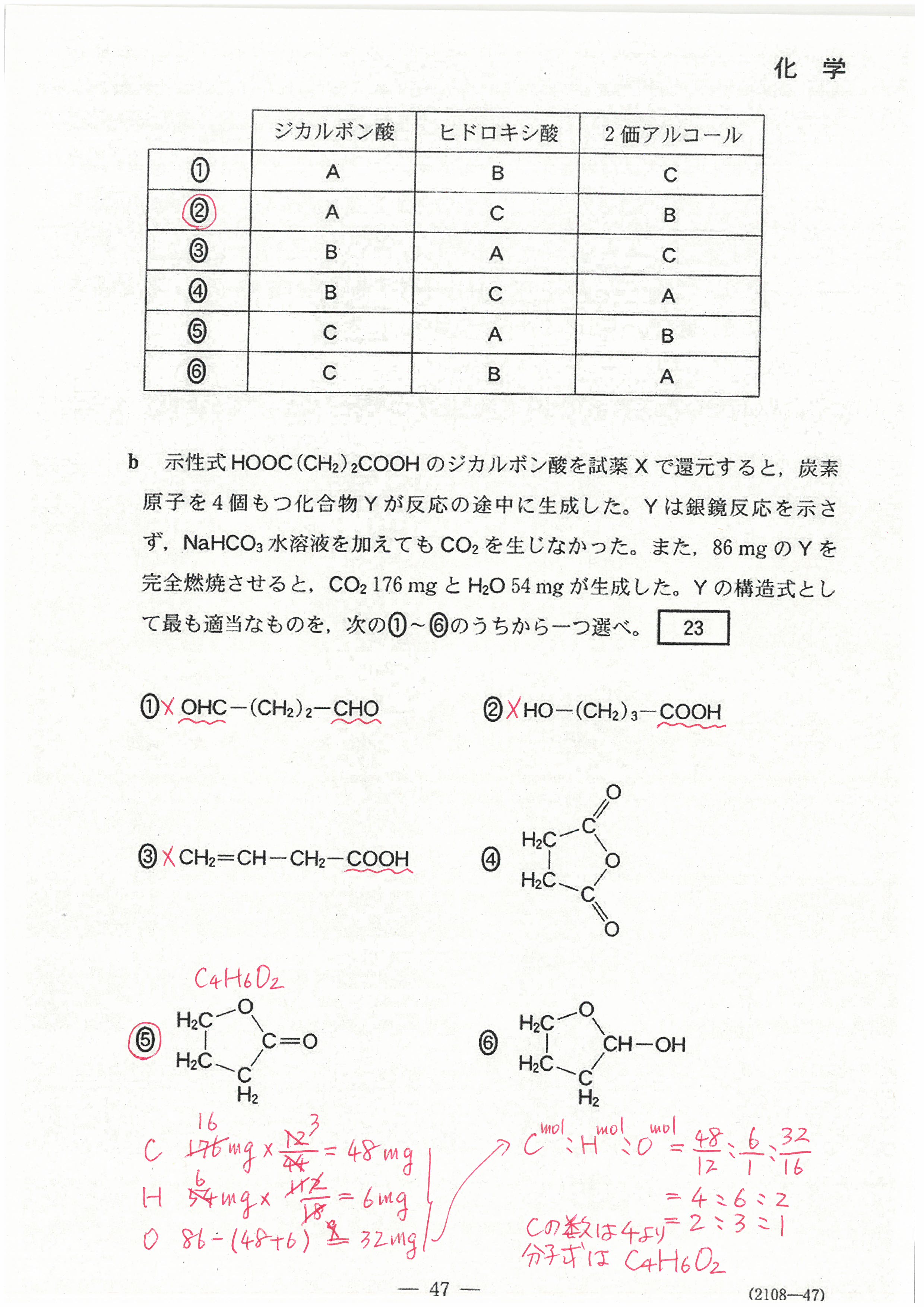
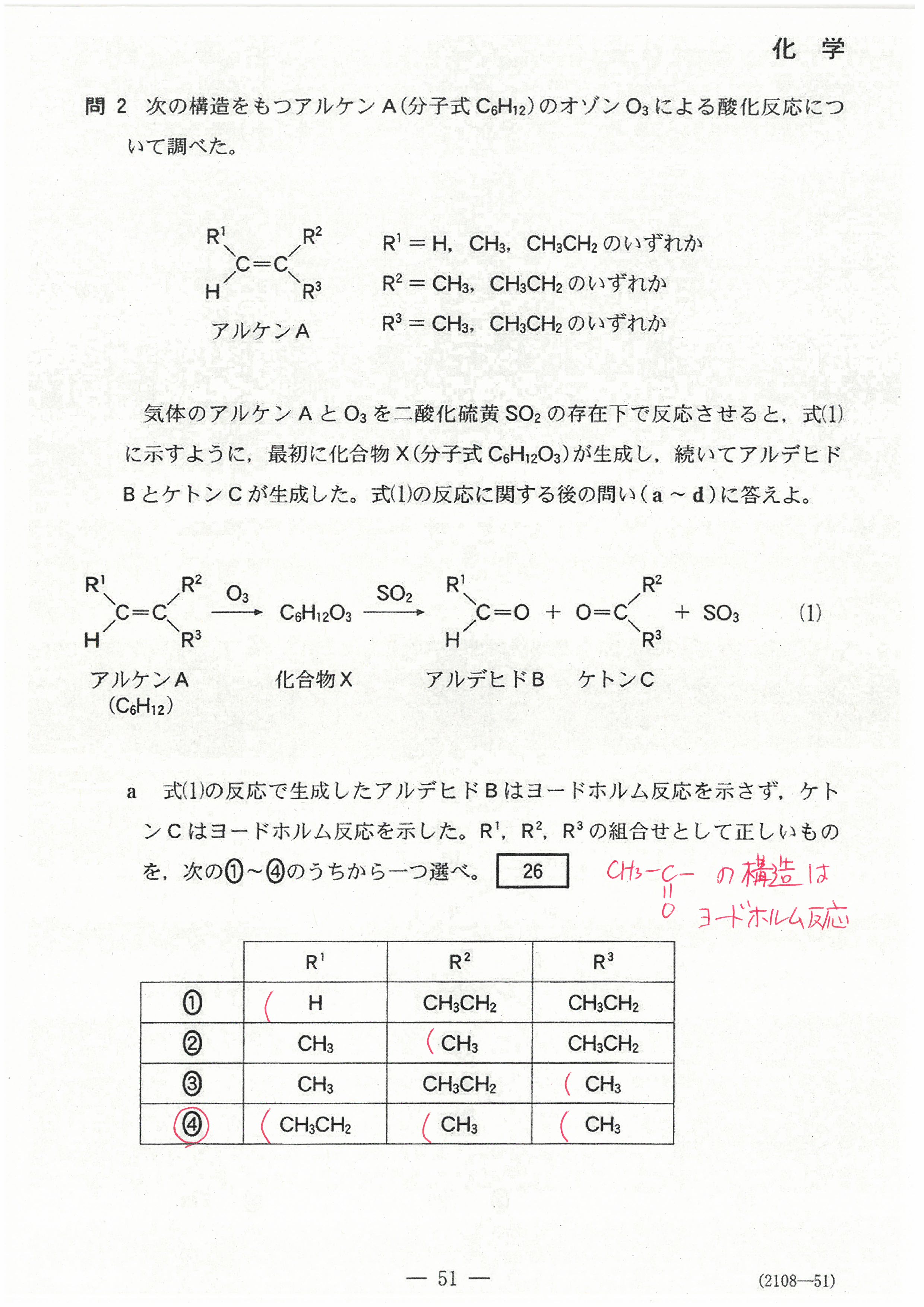
R4年度入学共通テスト(化学基礎)解答解説
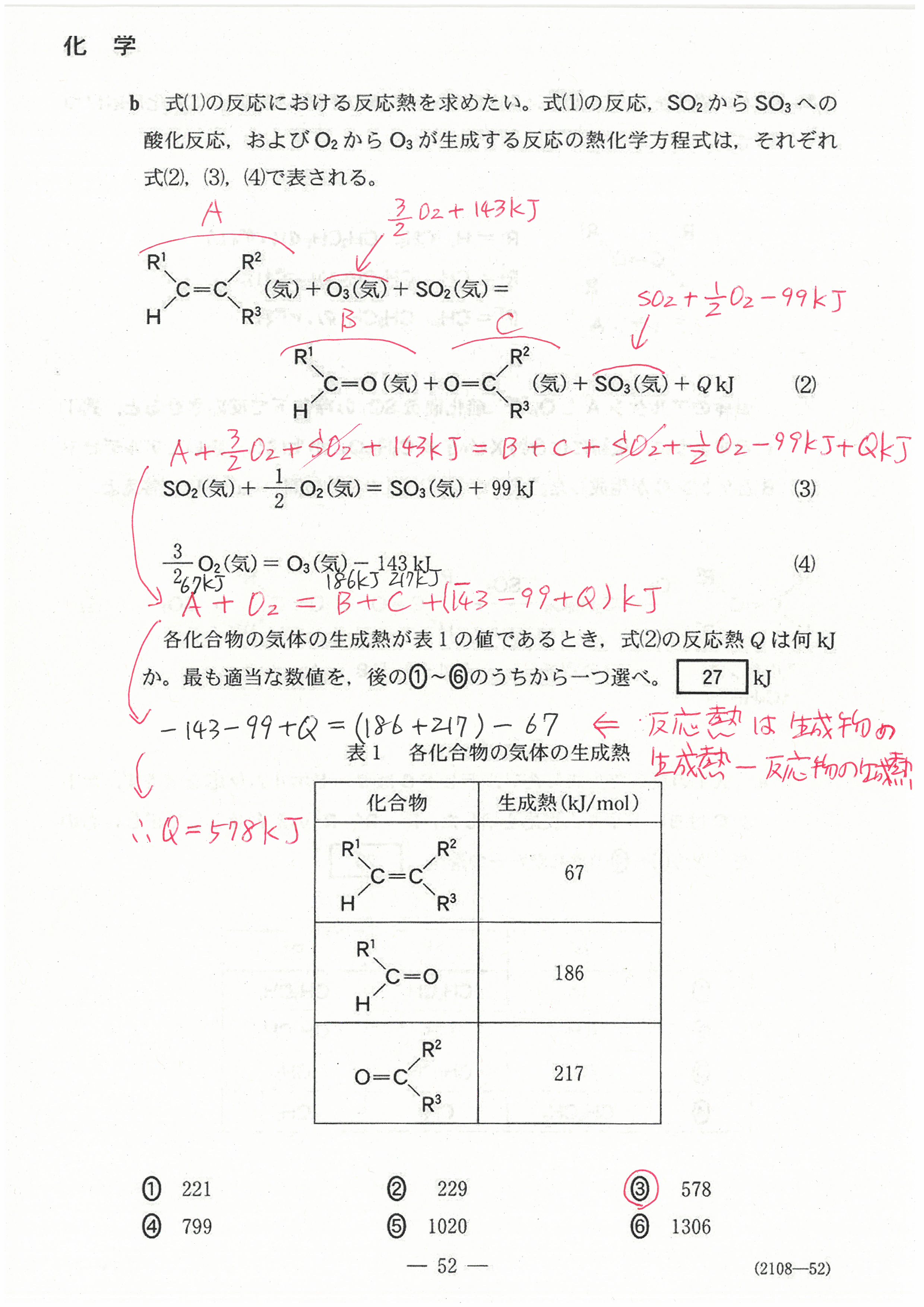
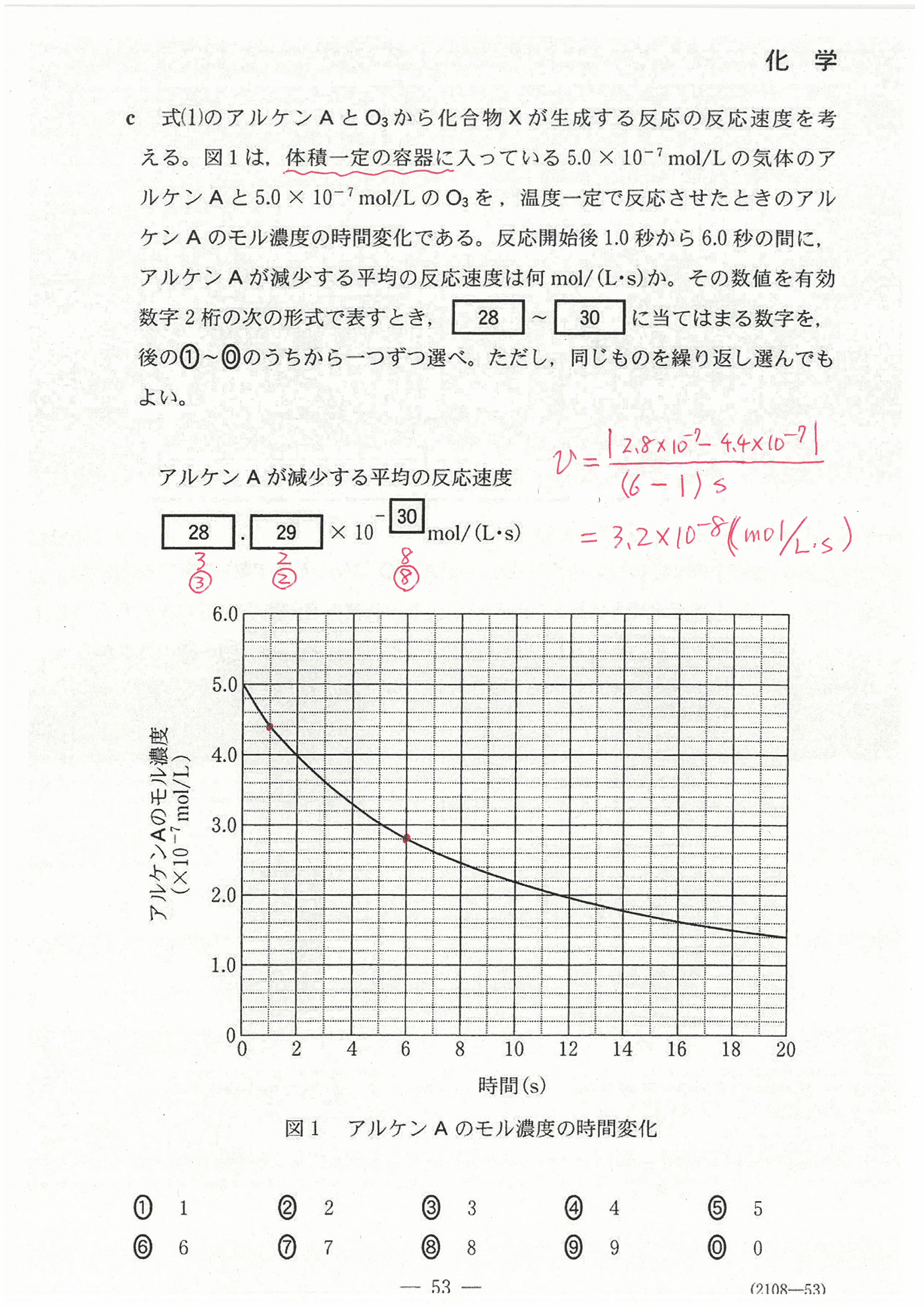
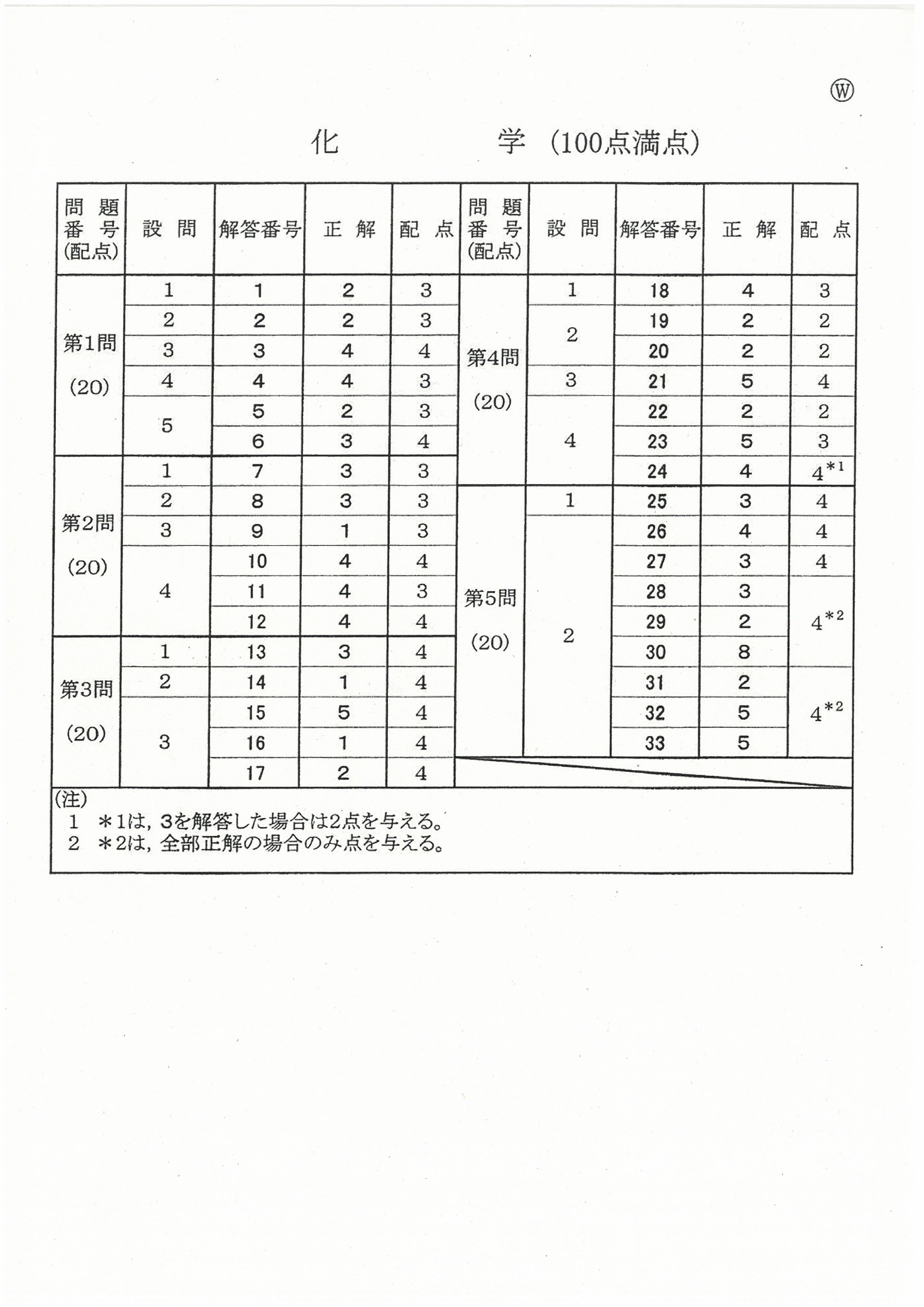
R4年度入学共通テスト(化学)解答解説
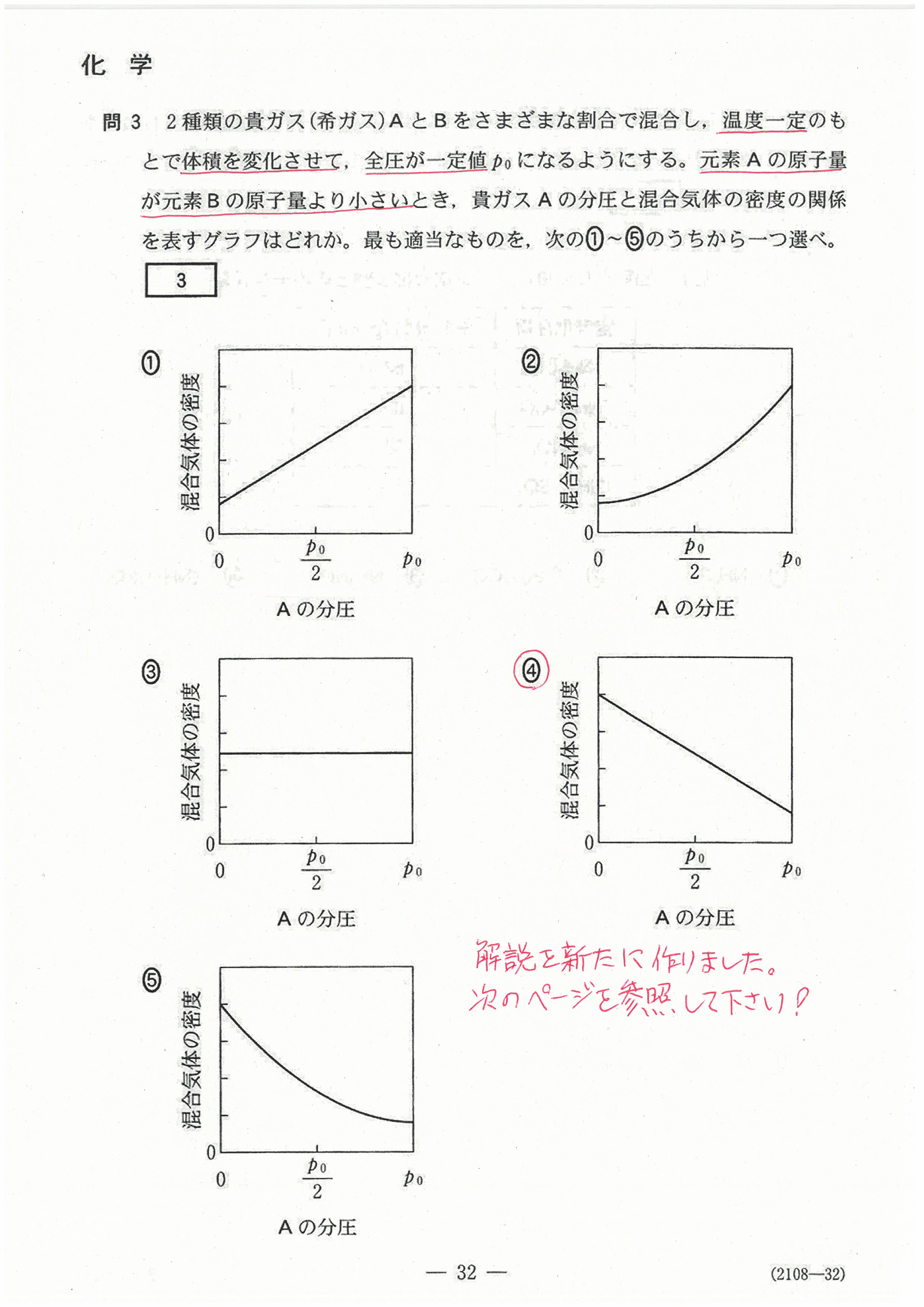
第1問の問3の解説を訂正しました!
最初の解説が間違っていたことをお詫びします。
申し訳ありませんでした!
桁が異なる単位同士の計算
これも新しいタイプの出題ですが、内容は難しくありません。
ここでは、桁が異なる単位の計算処理について書いてみたいと思います。
この問題では、雨水中の水素イオンH+の物質量(mol)を求めて、これと反応するCaCO3の物質量(mol)そして質量(kg)を計算できそうです。
では、まずH+の物質量(mol)を求めましょう。
H+(mol)=[H+](mol/L)× V(L)・・・①
上式のVは、降った雨水の体積(L)です。
そして雨水の体積Vは、雨が降った面の面積Sと降った雨の厚み(深さ)hから求められます。
体積V=面積S × 深さh・・・②
問題文中で、面積Sの単位は(km2)、深さhの単位は(mm)で与えられています。
体積Vを求める時に単位を揃えて計算しなければならないのはもちろんですが、最終的に体積Vはどの単位で表せばいいでしょうか?
(km3)?、(m3)?、(cm3)?、(mm3)?
ここで、(L)と(cm3)の換算、(L)と(m3)の換算がしばしば必要になるので、この換算の方法を覚えておいて下さい!
ということで、体積Vを(cm3)か(m3)で求めて、さらに(L)に換算することにしましょう。
では、これら2種の換算をこの問題の値で実際にやってみたいと思います。
【 体積を(cm3)で求めて(L)に換算 】
1.0(km2)=(1000 × 100cm)2=1010(cm2)
5(mm)=0.5(cm)
∴V=S × h=1010(cm2)× 0.5(cm)=5 × 109(cm3)
ここで、
1000(cm3)=103(cm3)=1(L)
よって、
V=5 × 109/103 = 5 × 106(L)
【 体積を(m3)で求めて(L)に換算 】
1.0(km2)=(1000 m)2=106(m2)
5(mm)=5 × 10-3(m)
∴V=S × h=106(m2)× 5 × 10-3(m)=5 × 103(m3)
ここで、
1(m3)=1000(L)=103(L)
をぜひ覚えましょう!
<1(m3)=(100cm)3=106(cm3)=1000(L)>
よって、
V=5 × 103 × 103 = 5 × 106(L)
どうでしょうか?
要は計算慣れしておけば難しくはないことが分かったのではないでしょうか?
では、式①のところに戻って、この問題を最後まで解いてみましょう。
pH=4より、
[H+]=10-4(mol/L)です。
∴ H+(mol)=[H+](mol/L)× V(L)
= 10-4(mol/L)× 5 × 106(L)
= 5 × 102(mol)
CaCO3 + 2H+ → Ca2+ + CO2 + H2O
より、H+と反応するCaCO3は、
5 × 102(mol) × 1/2 = 2.5 × 102(mol)
CaCO3=100(g/mol)より、
反応して溶け出すCaCO3は、
100(g/mol)× 2.5 × 102(mol)=2.5 × 104(g)
2.5 × 104(g) ⇒ 2.5 × 104/103
= 25(kg) 答 1⃣②、2⃣⑤
化学反応式の係数と量関係
化学反応式を書いて、それを元にして反応物や生成物の量関係を考える・・・
この量関係の考え方について、お薦めの方法を書いてみたいと思います。
このウェブサイトは、
NetCommons3.3.7で動いています。
NetCommons プロジェクト 開発の、
CMS+グループウェアです!
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
27 1 | 28 1 | 29 | 30 | 31 | 1 | 2 |
3 | 4 | 5 | 6 | 7 | 8 | 9 |
10 | 11 | 12 | 13 | 14 | 15 | 16 |
17 | 18 | 19 | 20 | 21 | 22 | 23 |
24 | 25 | 26 | 27 | 28 | 29 | 30 |