入試問題・模試問題 解説等
すぐに公式を使おうとせず、原理を考えるクセを!
これも新タイプの出題なんですが、ちょっと考えてみて下さい。
文の量は多いんですが、難しい内容ではありません。
公式を使って説明するなら、
Q=mcΔT 【Q(熱量)、m(質量)、c(比熱)、ΔT(温度差)】を使い、
この式を ΔT= Q/mc に変形して考えれば解けそうですね。
ですが、出来るだけ「考えながら解く」というスタンスで原始的にいってみましょう!
実験結果の「表1」を見て下さい。
塩酸を中和するために加えた水酸化ナトリウム溶液の量は、bはaの 1/2倍
ですから、
中和で生じた水の量も、bはaの 1/2倍
よって、
中和で生じた熱量も、 bはaの 1/2倍
一方、中和後の溶液の全体積について考えてみると、
a は 10 + 20=30cm3
b は 10 + 10=20cm3
中和後の溶液の全体積を比べると、
溶液の全体積は、 bはaの 2/3倍
です。
さて、溶液の温度上昇ですが、
発生した熱量が大きいほど温度上昇も大きくなります。
また、溶液の体積が大きくなるほど温度は上がりにくくなります。
よって、
溶液の温度上昇度は、
「発生した熱量に比例し、溶液の体積に反比例する」
と考えられます。
以上のことより
bの温度上昇度は、aの温度上昇度 × 1/2 × 3/2
となります。
∴ 2℃ × 1/2 × 3/2 = 1.5℃ 答③
フラーレンに関する新手の問題(3)
では、解説と解答を書いてみます。
解説中の価標について、まだ結合していない価標の数を「~手」、2原子間で結合している価標の数を「~本」、と記してあります。
Cから出ている価標の数は4手で、フラーレンC601分子中の60個のC原子から出ている価標の総数は、
4 × 60 = 240手
です。
2つのC原子間の2手の価標がつながって1本の価標になるので、C60分子中の「結合で出来上がっている価標」の数は、
240手/2 = 120本
となります。
一方、前問より、C・C間の結合の総数は、
[5,6結合]60本 +[6,6結合]30本 = 90本
です。
すると、
120-90=30本
この分の価標が余りますね?
この30本分の価標がC・C間の2本目の価標となり、その結果30か所に2重結合が出来るということになる訳です!
以上の結果、単結合が60本、二重結合が30本となりますね。
これでつじつまが合うことを確認して下さい!
フラーレンに関する新手の問題(2)
解説と答えを簡単に書いてみます。
5員環どうしは接しないので、5員環の周りは全て6員環ということになります。
5員環1個の周りには5本の[5,6]結合があり、5員環は12個存在しています。
よって、[5,6]結合の数は、
5本 × 12個 = 60本
また、6員環の周りには6辺あり、20個の6員環の辺の数は
6辺 × 20個 = 120辺
このうち、5員環との結合60本分つまり60辺を除いた分
120辺 ー 60辺 = 60辺
が6員環どうしの結合[6,6]結合の分となります。
2つの6員環の2辺が重なって[6,6]結合が1本出来ると考えれば良いので、
[6,6]結合の数は、
60辺/2 = 30本
となります。
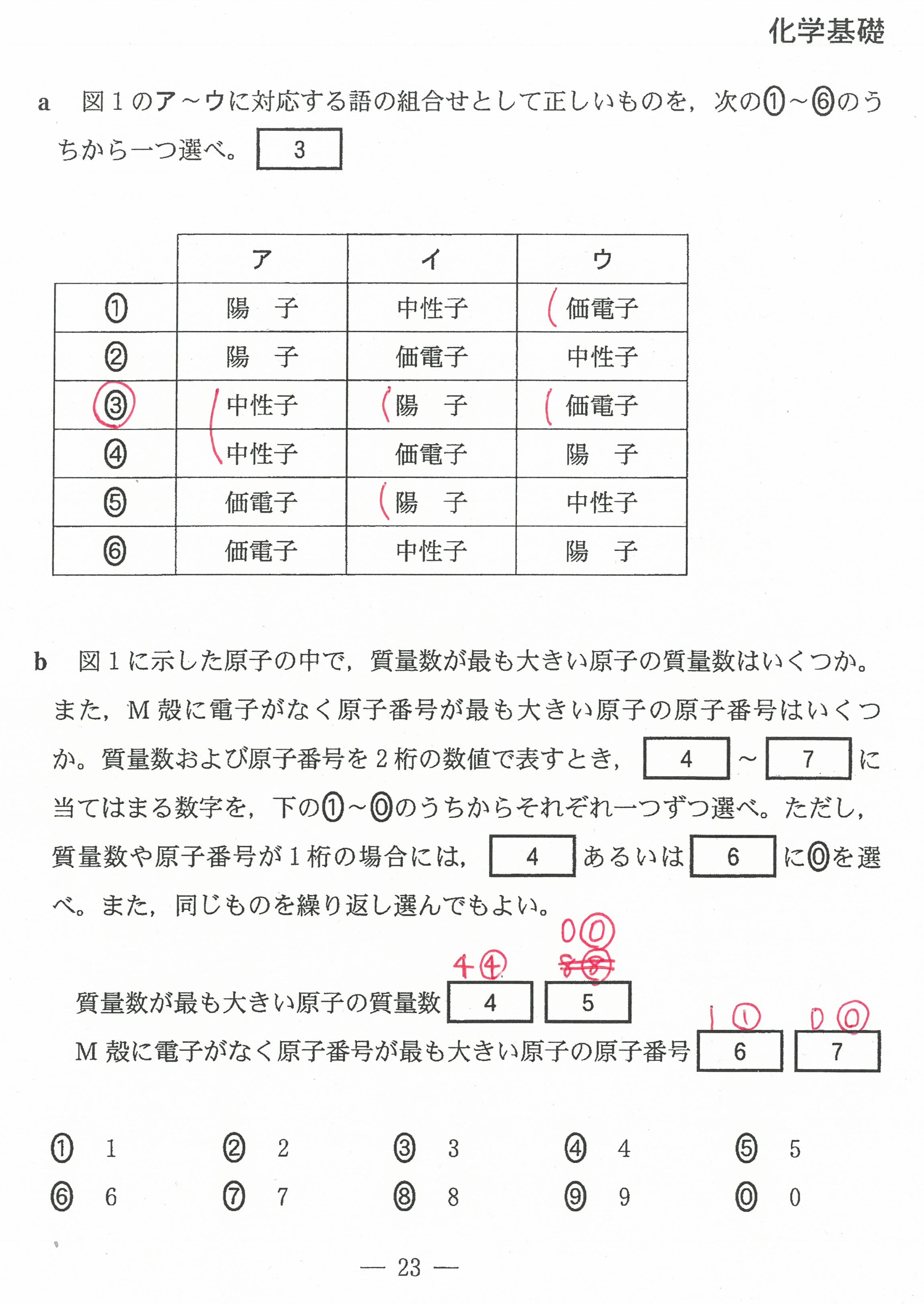
正解は、 1⃣ ③、2⃣ ⓪、3⃣ ⑥、4⃣ ⓪
ですが、3⃣、4⃣ を先に考えた方がいいですね!
さて、どうだったでしょうか?
この問題の続きがもう1問あるので、挑戦してみて下さい!
答えは次回に書きます。
フラーレンに関する新手の問題(訂正)
昨日紹介したフラーレンについての問題ですが、この問題文の前置きの文中に重要な条件が書かれていて、それを抜かしてしまっていました。
すみません!
条件文と合わせて問題文を再度載せます。
フラーレンに関する新手の問題(1)
フラーレンC60分子についての問題を解いてみて下さい。
まずは、教科書の例題と同様の問題です。
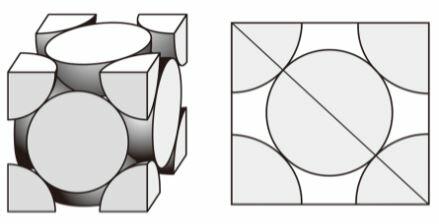
ここでは、単位格子を構成している粒子は何であっても同じ方法で解けるので、構成粒子がフラーレンであることは関係ありません。
単位格子1辺の √2倍が単位格子の面の対角線の長さになります。
そして、この対角線の長さの4分の1が粒子の半径ということになります。
下の図が分かりやすいでしょう。
∴ 1.41nm × √2 × 1/4 = 0.5nm 答①
さて、新手の問題というのは次の問いです。
考え方と正解は次回に書きますので、ぜひ挑戦してみて下さい!
考え方を提示されれば、「あーそうか!」となると思うんですが、化学の入試問題としては珍しいタイプなので、戸惑うのではないでしょうか?
自分はしばらく悩みました。
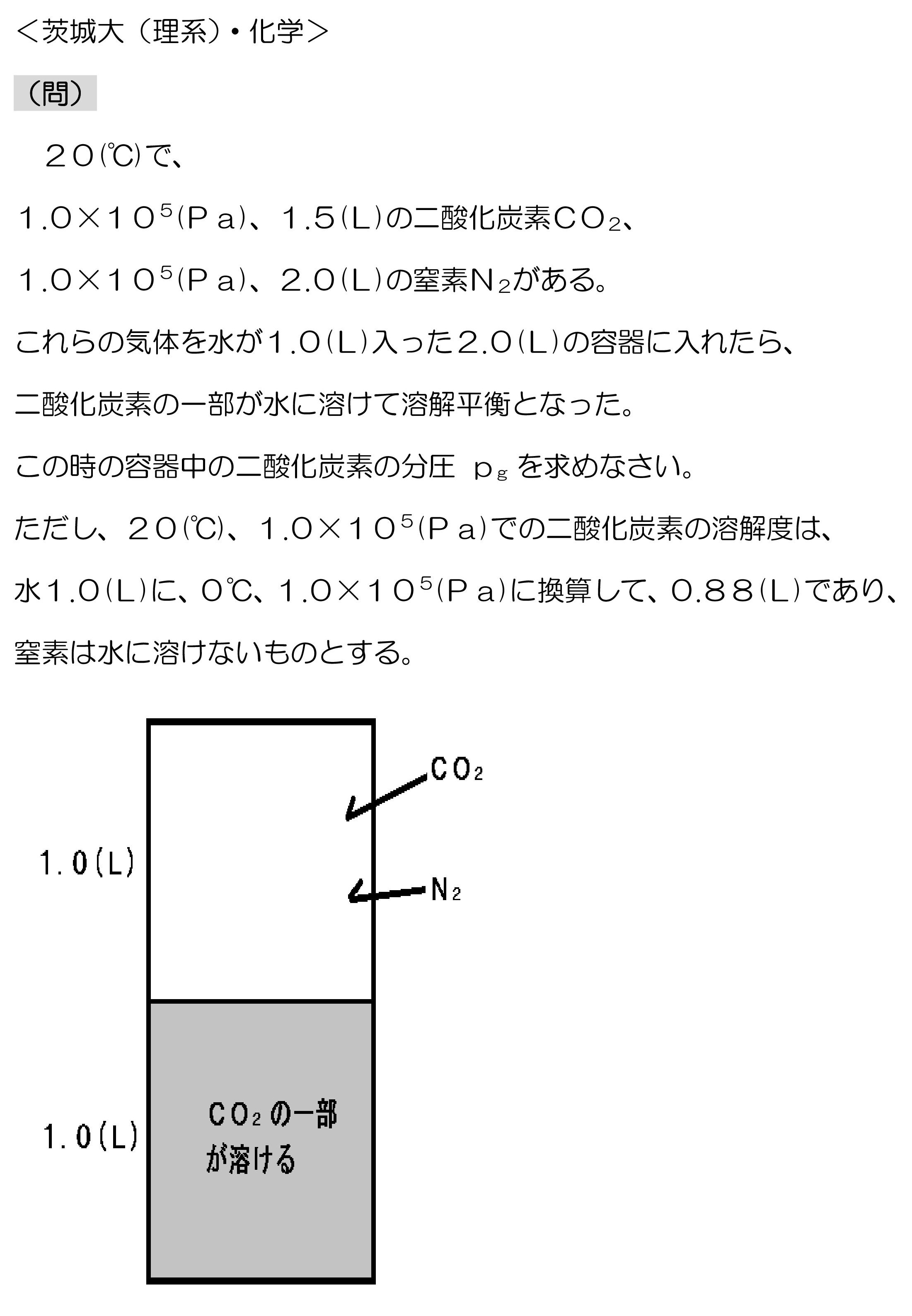
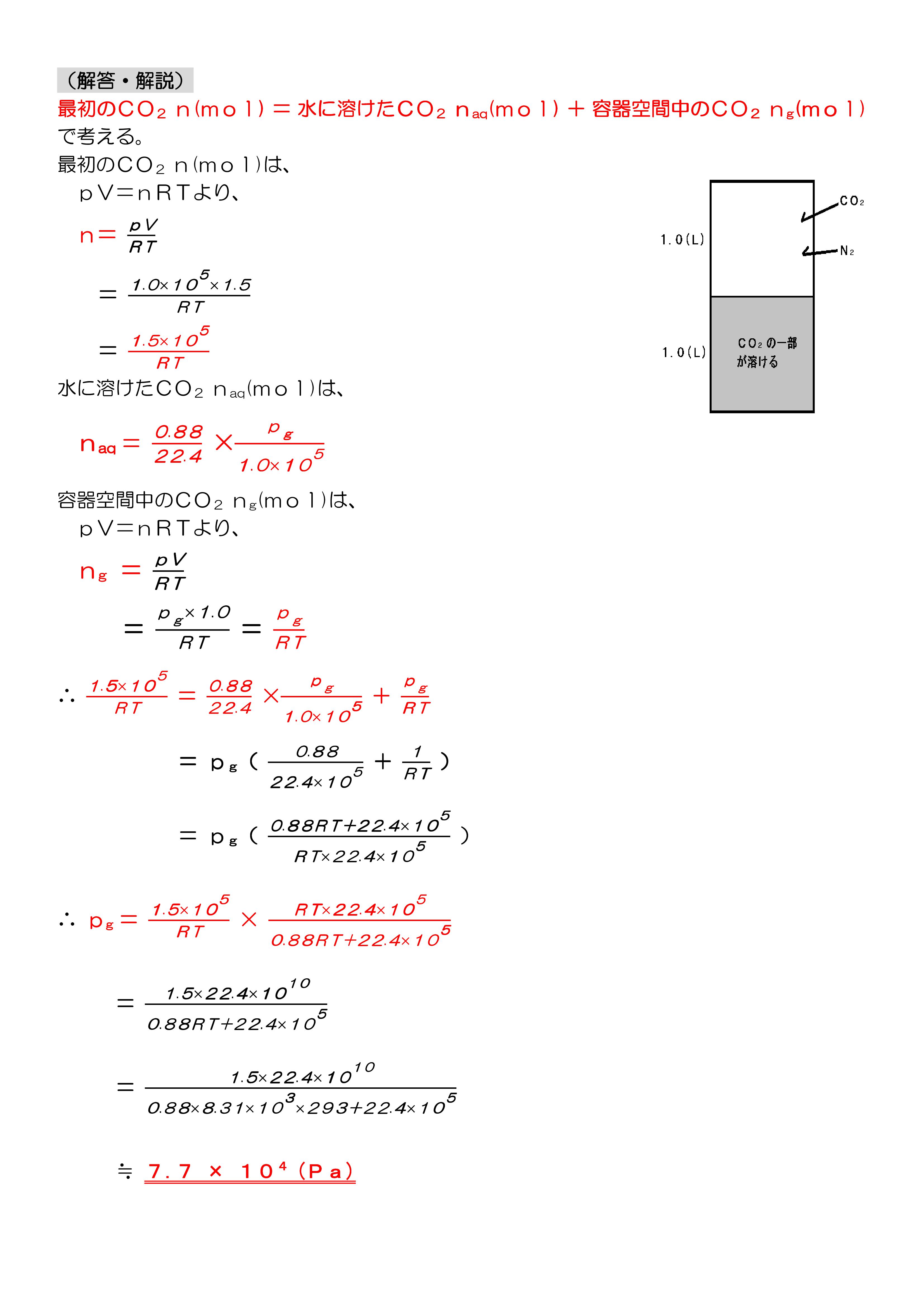
茨城大(理系化学・気体の溶解平衡)記述問題
この問題を解く時、「最初のCO2=水に溶けたCO2+容器空間のCO2」 がすぐに思いつかず、時間がかかってしまいました・・・
この問題では、封入したCO2に対して水に溶けるCO2がかなり多く、水に溶解するCO2の量を除いた分の圧力が容器空間内のCO2の分圧になります。
ここで、水に溶解するCO2の量は容器空間内のCO2の分圧に比例するところが厄介だと思うんですが、
「最初のCO2=水に溶けたCO2+容器空間のCO2」を使えば、式は簡単に作れるということです。
ただし、計算はかなり面倒です。
有効数字3ケタの値で計算していって、最後に有効数字2ケタに丸めなければなりません。
R=8.31×103、T=293(K)を使うので、共通テストのように簡単にはいきませんね。
これは過去問ですが、最近は計算がもっと楽になるようにしてくれていると思うんですが・・・
(ごめんなさい。確証はないんですが)
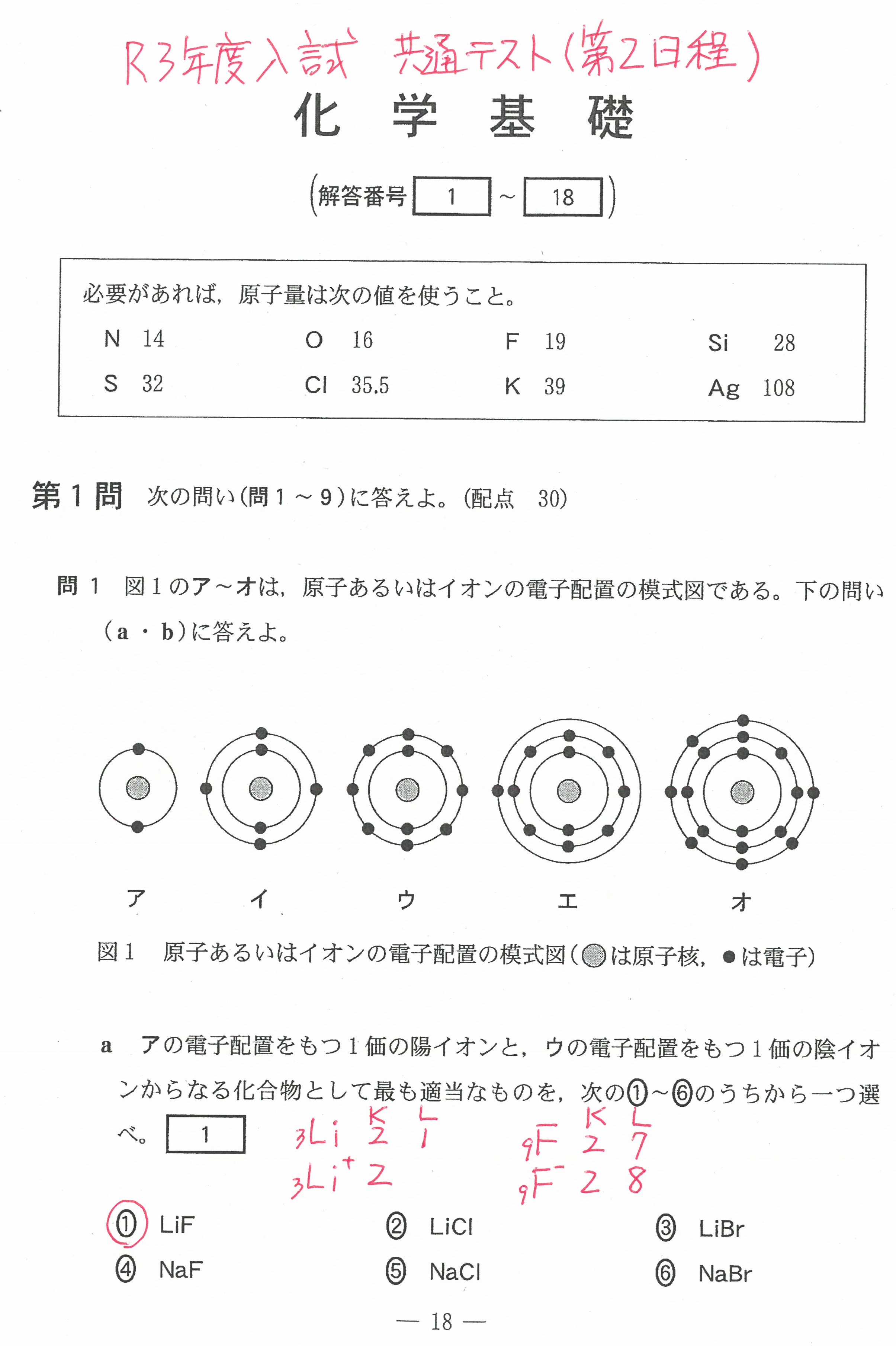
R3年度入学共通テスト第2日程(化学基礎)解答解説
R3年度入学共通テスト第2日程(化学)解答解説
R3年度入学共通テスト(化学基礎)解答解説
R3年度入学共通テスト(化学)解答解説
このウェブサイトは、
NetCommons3.3.7で動いています。
NetCommons プロジェクト 開発の、
CMS+グループウェアです!
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
27 1 | 28 1 | 29 | 30 | 31 | 1 | 2 |
3 | 4 | 5 | 6 | 7 | 8 | 9 |
10 | 11 | 12 | 13 | 14 | 15 | 16 |
17 | 18 | 19 | 20 | 21 | 22 | 23 |
24 | 25 | 26 | 27 | 28 | 29 | 30 |